Alternatives to Mainstream Fusion

This website has concluded that the mainstream approach to commercial fusion reactors will likely fail for the following main reasons.
- Enormous physical size leading to high cost,
- Low availability due to necessity for frequent component replacement due to radiation damage,
- Scarcity of tritium fuel requiring regeneration in power plant operation and problems with start-up stock.
Alternative fusion technologies, many of which were tried and discarded decades ago, have recently reappeared to solve these problems. Figure 1 shows the numbers of fusion devices of different types, operational and in construction/planning, in 2022. Currently there are 54 operational tokamaks and 12 operational stellarators. In addition there are 11 operational inertial fusion devices and 22 devices with various other technologies labelled as "Alternative Concepts".

Figure 1. Data from World Survey of Fusion Devices, 2022, IAEA. DEMO (Demonstration Power Plants) planned, and Exp (Experimental Devices) planned, under construction and operating.
For evaluation purposes these alternative technologies, are divided into three different classifications: "Toroidal", "Aneutronic" and "Pulsed" devices. The toroidal class covers all devices closely related to mainstream fusion. The aneutronic class postulate the use of alternative fuels to D-T, in an attempt to avoid radioactivity. The pulsed class defines a shared property of the devices concerned, as having a duration of fusion reactions less than one second.
Many of the developments of these alternative technologies are now being undertaken by private companies rather than by publicly-funded research institutions as in the past. Table 1 gives details of 26 private fusion companies which each have accumulated funding >$5 million, taken from the Global Fusion Industry Report. Figure 2 shows the growth of the number of these companies the first of which appeared 25 years ago but which has had a very significant increase during the past 8 years.
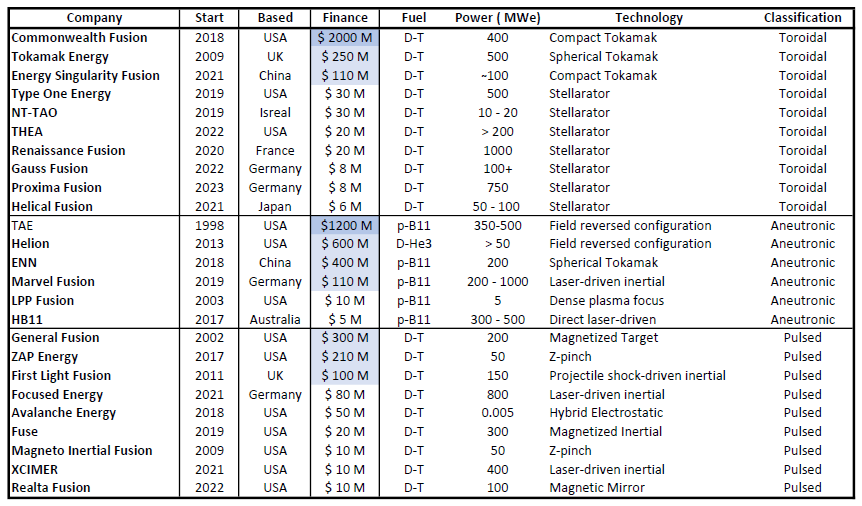
Table 1. Details of the private fusion companies each of which has accumulated funding > $5 million (adapted using data from Global Fusion Industry Report). The column "Power" gives the answer, from the fusion company, to the question: "Anticipated Megawatt electricity output (MWe) of your commercial operating facility?" and the number may be open to some doubt. The presentation of the table separates the devices into classifications of "Toroidal", "Aneutronic" and "Pulsed" which are described in the text. The table only includes companies who's primary business is to develop technologies to produce electricity.
The power values given by the fusion companies and listed in table 1 are important but have a very wide range which is difficult to understand. It could be that some replies pertain to an envisaged facility with multiple devices rather than the power for a single device. On this page are some estimates of what would seem possible for devices in a particular class.
Figure 2 shows the growth of the private companies. The companies developing Aneutronic and Pulsed devices started to appear from 1998 while the class Magnetic, which has technologies closest to the mainstream fusion started to appear later, with a big boost in 2017.
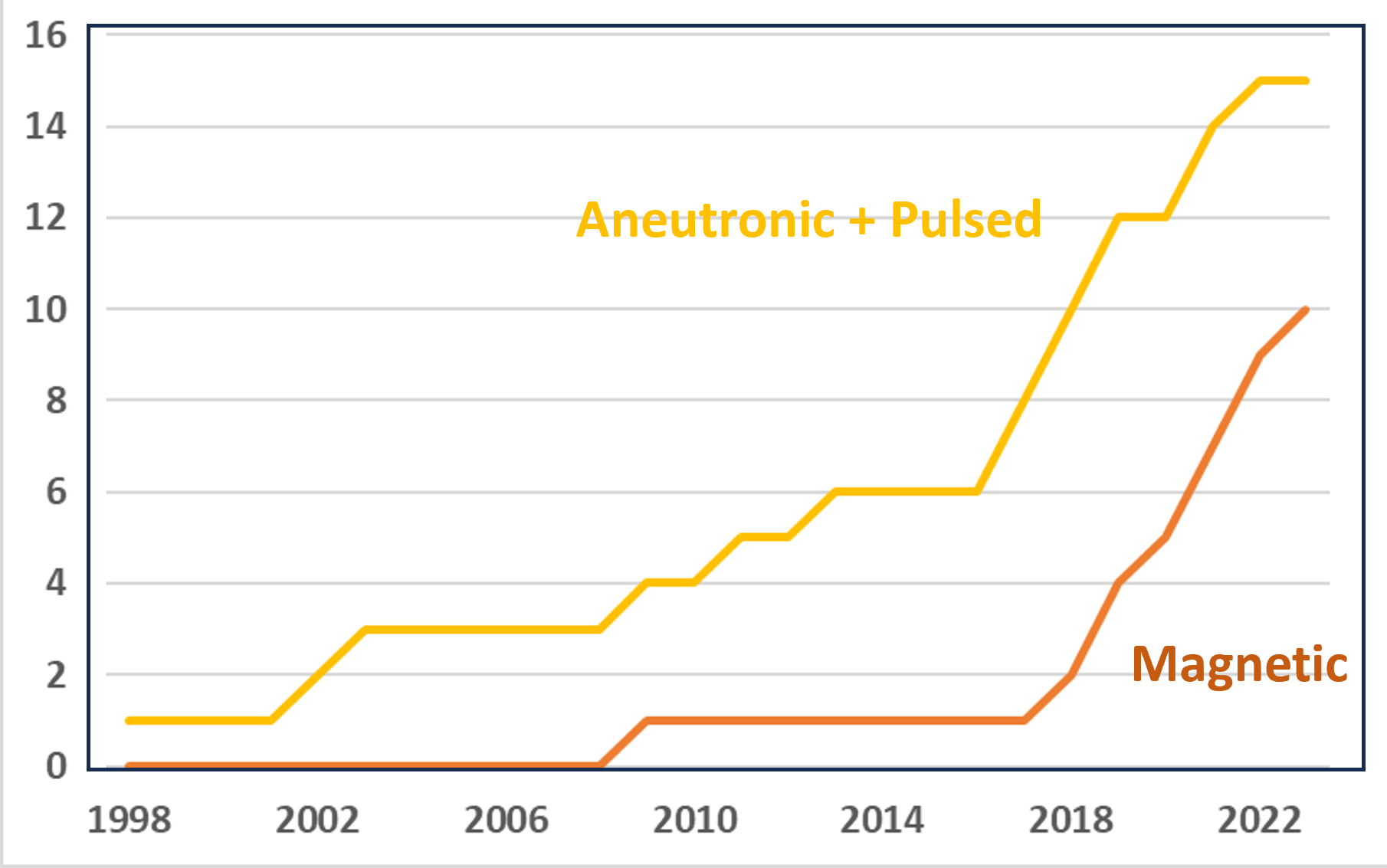
Figure 2. Growth of private fusion companies each having accumulated funding of >$5 million since their foundation. The brown curve shows companies classed as Magnetic in table 1 and the yellow curve is all the others.
This feature of private company involvement in current fusion research is now widely reported in the media but in a way which lacks any critical evaluation of the relative merits of the diverse devices being considered. Daniel Jassby has written on essay on the problem: Documents. The objective of this page and the subsequent pages is to provide such an evaluation.
Toroidal Devices
The first class of fusion devices discussed is termed "Toroidal" (effectively an abbreviation for "Toroidal Magnetic Confinement Fusion"). This class contains 10 of the 26 companies listed in table 1. The specific technologies adopted by the companies are: compact tokamaks; spherical tokamaks and stellarators.
Size Optimization
This aims to identify the fusion device parameters which must change to reduce size and device cost. Although many of the private companies advertise cost reduction through the use of higher magnetic fields, the most important parameter affecting device cost is the acceptable power load on the wall surrounding the plasma, the "first wall. In devices using D-T fuel, energy is carried out and into the first wall by action of neutrons escaping the plasma.
1) Simple estimate of device power output
Figure 3 gives an estimate of the power output on toroid size using just the single parameter of limiting first wall power flux, Pwall, using the simple calculation. explained in the inset. This calculation assumes an efficiency for the conversion of the output fusion power to output electrical power of 40%.
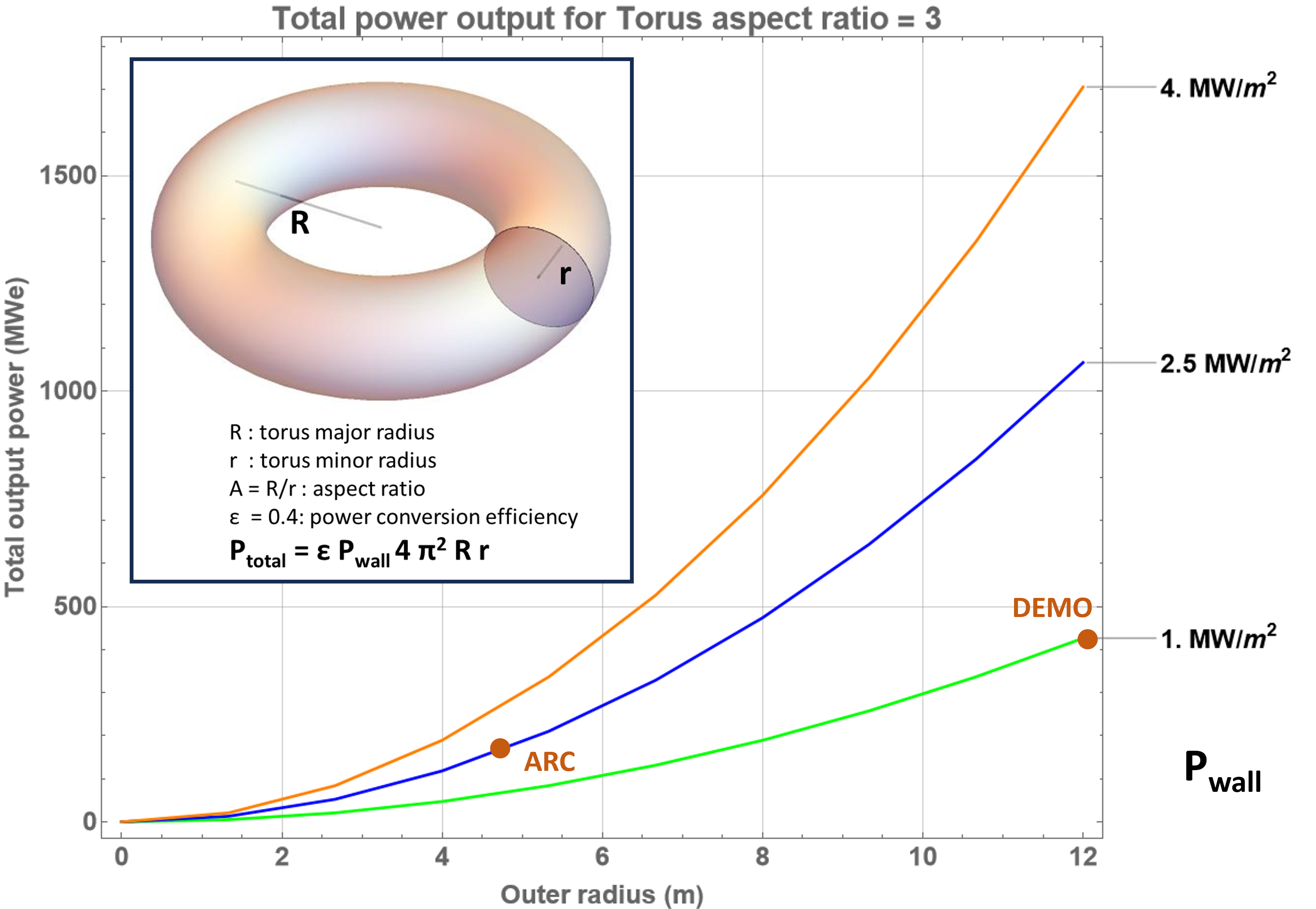
Figure 3. Simplified calculation of the power output of a toroidal fusion device, with aspect ratio R/r = 3, as a function of device device vacuum vessel outer radius (=R+r), based on the parameter of limiting first wall power loading taken as 1 MW/m2 (value of DEMO design), 2.5 MW/m2 (value of ARC design) and 4 MW/m2 (an estimate of the upper limit possible). The design points of the DEMO and ARC designs are marked.
The DEMO (planned mainstream tokamak power plant) design currently postulates a first wall power loading, Pwall , of around 1 MW/m2 and the ARC (planned private fusion company power plant) design has 2.5 MW/m2 with outer radii 12 m and 4.4 m, respectively. The electrical power from the graph for both tokamaks are about 30% lower in this very simple calculation than in the real design evaluations, partly because the real devices will have "D" shaped rather than circular cross-sections. The graph shows that an ARC type device the same size as DEMO could attain a 1 GWe power output, twice that of DEMO, but would still be a very large machine.
A power load of 1 MW/m2 deposited by neutrons in the first wall and breeder blanket (described for mainstream tokamaks at: Breeder blanket) would be expected to raise the structure temperature by about 1 °C/sec. A high enough coolant flow is required to remove this heat and constrain the maximum temperature of the first wall. How realistic a given Pwall value is depends on the detailed design of the cooling system. At 1 °C/sec it is believable that the DEMO design would work and also at 2.5 °C/sec that the ARC design with liquid metal coolant could work, however going beyond 10 MW/m2 implying 10 °C/sec temperature rise seems unworkable. It should be noted that tokamak designs must also allow for the instantaneous heat load imposed on the first wall by the disruptions causing rapid plasma loss.
2) Detailed analysis of tokamak optimization
This section presents a summary of a detailed analysis of tokamak optimization which likely applies also to other toroidal magnetic confinement devices.
The paper of Freidberg et al., Designing a tokamak fusion reactor, evaluates the cost optimization of tokamak reactors including the dependence on magnetic field. This paper defines a measure of the tokamak cost as the ratio of the volume of highly engineered reactor components (VI) to the electric power output (PE), which was originally introduced by Spears and Wesson in Scaling of tokamak reactor costs. Figure 4 shows the contributions to the volume, VI. The volume of the plasma is given by the requirements of plasma confinement and depends strongly on the magnetic field, Bmax. The breeder blanket thickness, b, is fixed by the nuclear physics of stopping the 14 MeV neutrons and has a minimum of about 1.2m. The thickness of the Toroid Field (TF) magnet is defined by the structural material required to balance the mechanical stress on the coils due to the magnetic field.

Figure 4. Components of highly engineered volume used in the tokamak cost optimization of Friedberg et al. The thickness of the breeder blanket (b) and the Toroidal Field (TF) magnet with its support dominate the cost of the tokamak.
Figure 5 shows the dependence of the cost measure VI/PE for variations in the wall power PW and maximum magnetic field, Bmax , when all other tokamak parameters are held constant.

Figure 5: Results from the cost optimization of Friedman et al, showing the cost measure VI/PE as function of the wall power PW and maximum magnetic field, Bmax, when all other tokamak parameters are held constant.
The left plot in figure 5 shows that the first wall power load is the critical parameter in tokamak cost optimization: increasing the allowable power load from 1 MW/m2 to 5 MW/m2 could reduce the cost by a factor four. In contrast, increasing the maximum magnet field from 10 T to 25 T would actually increase the cost by 50% because of the extra structural material necessary to support the magnetic stresses in the toroidal field coils.
This more detailed analysis of tokamak optimization confirms the simple-minded estimate of the dominant importance of the first wall power load.
Aneutronic Fusion
The second class of new fusion projects is that of aneutronic devices which propose to use alternative fuels to deuterium-tritium in order to avoid issues of radioactivity. In the private fusion projects of table 1, 6/26 are aneutronic.
A major problem for mainstream fusion given above, is the need to frequently replace components due to the impacts of 14 MeV neutrons from the D-T reactions. These neutrons lead to radiation damage, weakening structural materials, and to large volumes of radioactive waste generated by neutron activation of materials in tokamak components.
The third problem, also mentioned above, relates to the scarcity of tritium. The aneutronic fusion projects propose to solve both these problems by using fuel mixes which do not use tritium and do not produce neutrons.
Alternative Fuels
The four fusion reactions frequently considered for energy production are shown in figure 6. The aneutronic fuels with no neutrons emitted are D-He3 and p-B11. The D-D fuel has two different reactions, one which is aneutronic and the other which emits neutrons, so on average the fuel is not aneutronic. In practice in a device with D-He3, D-D reactions would also occur, so this fuel is not completely aneutronic either.

Figure 6: The four fusion reactions considered for fusion power reactors: D-T; D-D; D-He3 and p-B11. The two aneutronic reactions are D-He3 and p-B11. The D-D reaction has two possible final states with equal probabilities, one with a neutron and one without.
The massive drawback for p-B11 fuel is Bremsstrahlung (a.k.a. "braking" or deceleration radiation) which is illustrated schematically in figure 7.

Figure 7. Schematic of Bremsstrahlung (braking radiation) emitted when a charged particle is deviated by the electric field of a nucleus. The magnitude of the emitted flux of γ-rays and x-rays depends on the square of the nuclear charge and so is much higher for boron than hydrogen or helium.
The energy balance in fusion is well explained in the blog of Nick Hawker: Why does fusion need to be so hot? which gives a clear presentation of the dilemma for aneutronic fusion. To achieve net fusion power output the power generated by fusion, Pfus must be greater than the power lost by radiation, Prad. The snag for p-B11 fuel is that the electric charge, Z, for boron is 5 units compared to 1 for tritium so that the Bremsstrahlung radiation in the plasma is much higher to the point where the net energy gain is never positive. Figure 8, gives the power balance for the four fusion fuels as a function of plasma temperature in units of keV. Table 2 summarizes the maximum ratio of Pfus/Prad from the calculations of Nick Hawker and two other sources. All calculation show that the p-B11 fuel can never have a net fusion power gain.
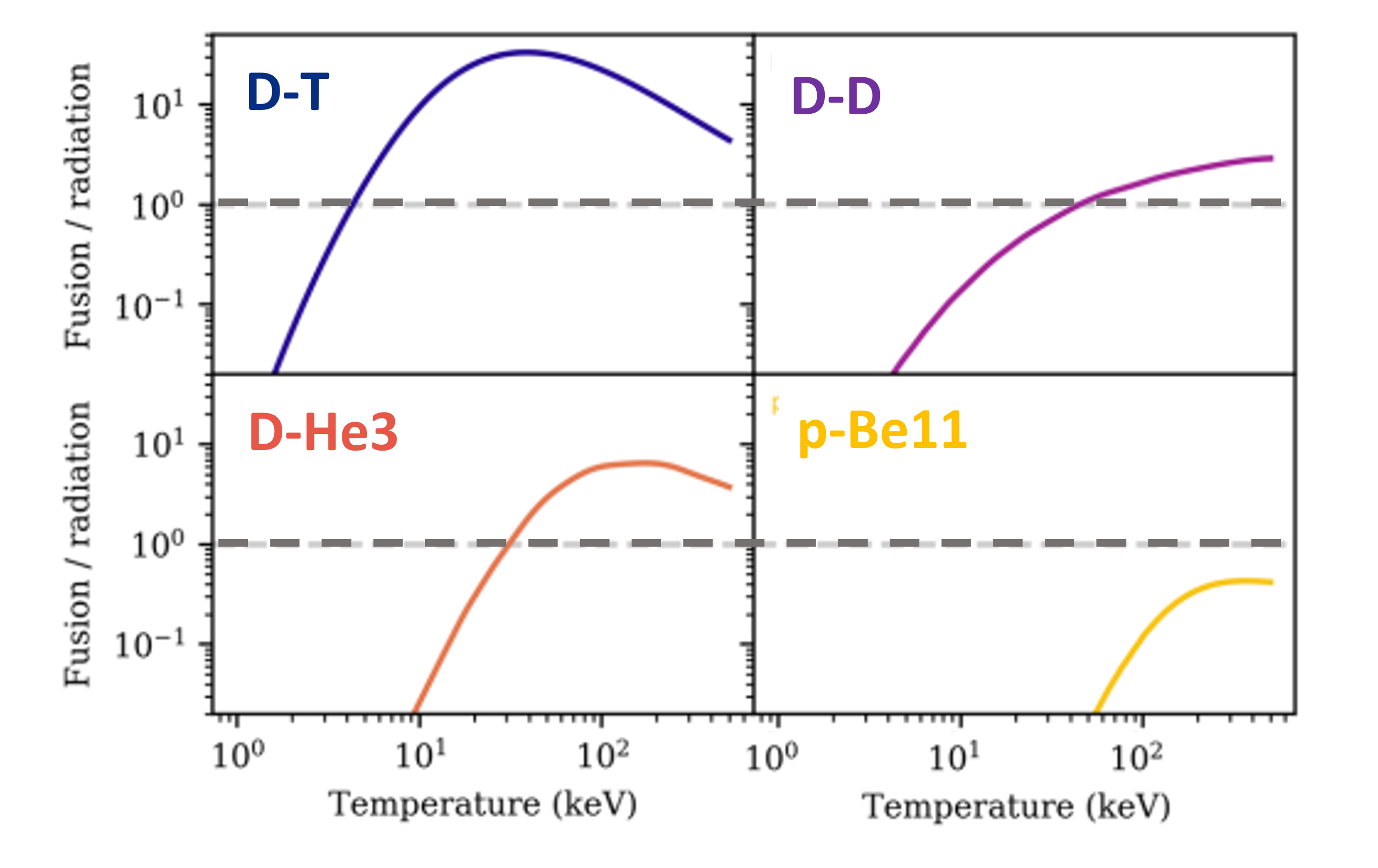
Figure 8. Ratio of Fusion power to the radiation loss plotted vs temperature in keV (1 keV = 12 million °C), for each of the four fuels. For p-B11 the fusion power never exceeds the radiation loss at any temperature. (From blog of Nick Hawker)

Table 2. Ratio of fusion power (Pfus) over radiated power (Prad) from Hawker and other calculations Parisi & Ball and Rider.
Beyond the references in table 2, there is further extensive literature on the prospects of p-B11. The paper of Nevis, A Review of Confinement Requirements for Advanced Fuels, concludes that ignition is impossible in p-B11. The paper of Putvinski, Ryutov and Yushmanov of TAE Technologies, Fusion reactivity of the pB11 plasma revisited, makes new calculations with updated cross-section but concludes that while ignition is still marginal, p-B11 remains a viable fusion fuel.
The data in figure 8 and table 2 suggest that D-He3 fuel could produce net fusion power, even though less than D-T and at higher temperatures. However as already mentioned, the presence of deuterium in the fuel mix means that as well as the D-He3 reaction, D-D reactions would take place producing either neutrons or tritium. If it not removed, the tritium will also produce D-T reactions producing yet more neutrons. By these mechanisms, the total power in neutrons from D-He3 fuel can be up to 5% of the total , so D-He3 fusion is not completely aneutronic. A further problem with D-He3 fuel is that helium3 is extremely rare on Earth, with all current supplies actually coming from the decay of tritium, so D-He3 fusion does not solve the tritium supply problem in a simple way.
In fusion devices with aneutronic fuels and so no neutrons, a major issue is getting out the power initially carried by charged particles and X-rays. This subject will be dealt with on the dedicated page: Aneutronic Fusion .
Pulsed Devices
A "pulsed" device is defined to be a device in which the plasma fusion exists for a period less than a few seconds. Nine companies in table 1 are classed as developing pulsed fusion technology, but in addition many of the aneutronic devices are also proposed to be pulsed, meaning the majority of candidate devices in table 1 use some kind of pulsed technology. The technologies of these projects are very diverse, however, ranging from laser inertial confinement to Z-pinch devices: figure 9 illustrates two examples of such devices. The diverse technologies of this class will be will be discussed in detail in subsequent pages: this page will evaluate the common pulsed property.

Figure 9. Images of two examples of "Pulsed" fusion projects: Focus Energy and ZAP Energy. The target areas in both devices have dimensions of about 2 m.
The essential parameter for all pulsed devices is their possible repetition rate in a fusion power plant. The National Ignition Facility (NIF) laser inertial fusion project at present produces about 1 MJ of energy with a pulse operation once every few months. To produce a 100 MW power plant, with the same energy per pulse, the repetition rate must increase to 100 times per second. At present, all other pulsed fusion devices are also likely to have very low repetition rates, as well as having zero exploitable energy output. This class of devices has the common feature that their publicity is very optimistic but lacking in vital details.
For all pulsed devices:
Total power output = Energy per pulse x Repetition rate.
Increasing the energy per pulse compared to the NIF 1 MJ might be possible but increasing the repetition rates would require different technologies to those presently in use. It is likely all pulsed devices will be limited by repetition rates.
An analysis of realistic power output from pulsed devices, independent of repetition rate limitations, is presented in figure 10. This plot is analogous to figure 3 for toroidal devices, being based on the the device power output limitation from the allowable power flux through the first wall interface, Pwall. This analysis considers that the pulsed devices all have the common feature that the fusion takes place in a small region surrounded by an interface, the first wall, which can be approximated as a sphere.

Figure 10: Simplified calculation of power output for a generic "Pulsed" device assuming the fusion region of the device is approximately spherical and relatively small.
From the plot it can be seen that devices with 2m-dimensioned fusion regions will be limited to 50 MWe power output with first wall power loads limited below 2.5 MW/m2. The aneutronic projects claim a higher power conversion efficiency than the assumption in this plot, so if these projects can make the p-B11 fuel work as well as a highly efficient energy conversion technique, then they could attain a 100 MWe device. With these numbers, the upper range of the power outputs given by the private companies in table 1, seem wildly unrealistic.
Conclusion
The conclusion of this page is that only the "Toroidal" class of fusion devices has any chance of commercial success. The new compact technologies might reduce the size of devices by a factor 1.3 (from figure 3) and so the cost by a factor 2, but only by increasing the first wall power loading limit and not by increasing the magnetic field.
The "Pulsed" projects, if they can increase their repetition rates dramatically, are never likely to build large capacity power plant, greater than 50MWe, because of their small size.
The "Aneutronic" projects are very unlikely to succeed with the alternative fuels and because of their pulsed nature would anyway be unable to produce significant power output.
This page has used generic arguments to evaluate the three defined classes of fusion devices. Subsequent pages on this website discuss the projects of these private companies in more detail: